思路
因为题目所说数组是严格单调递增的,因此如果说nums[0] < nums[len - 1]那么nums[0]一定是数组的最小值。
那如果不是呢?应该如何考虑,如下图所示 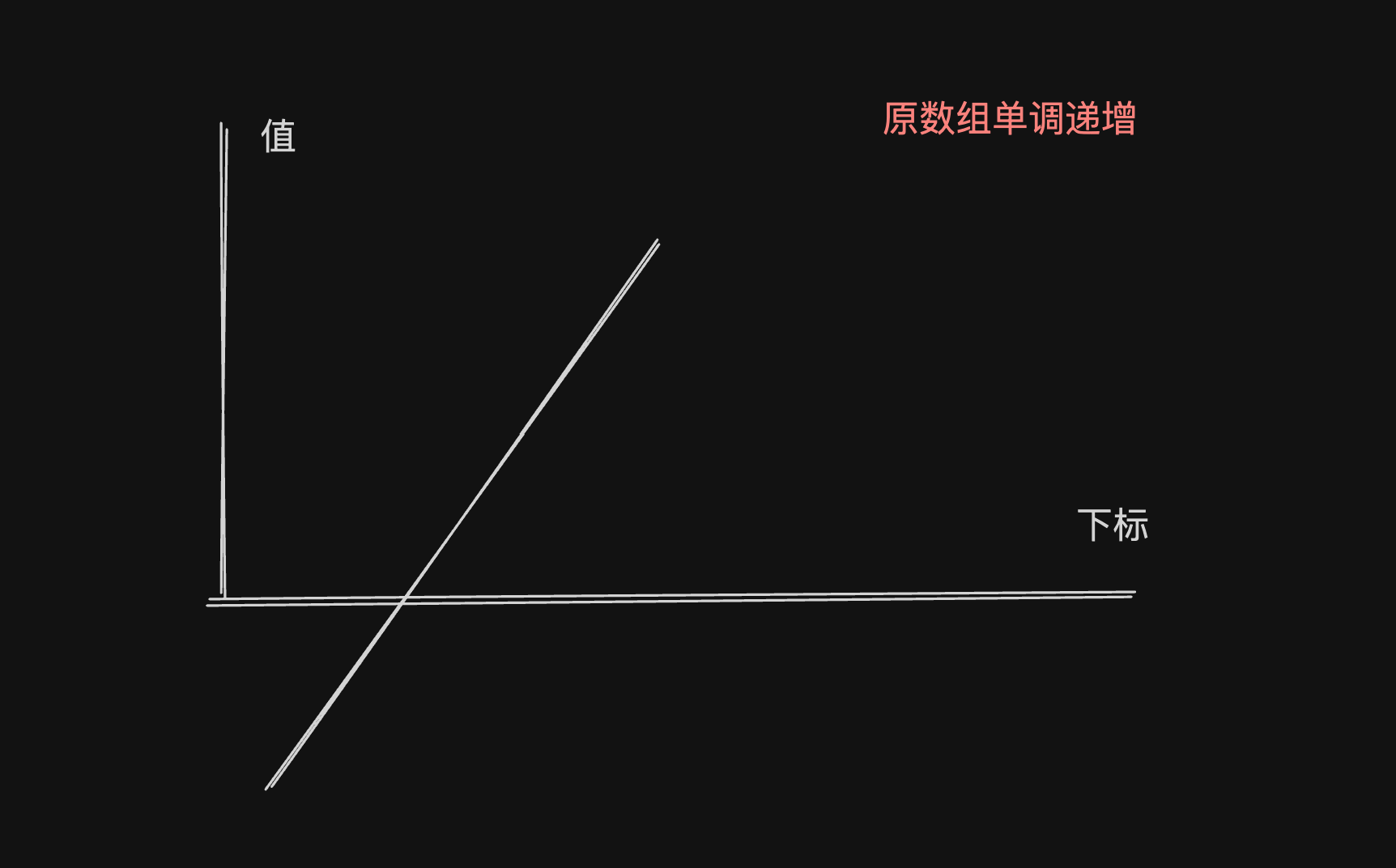
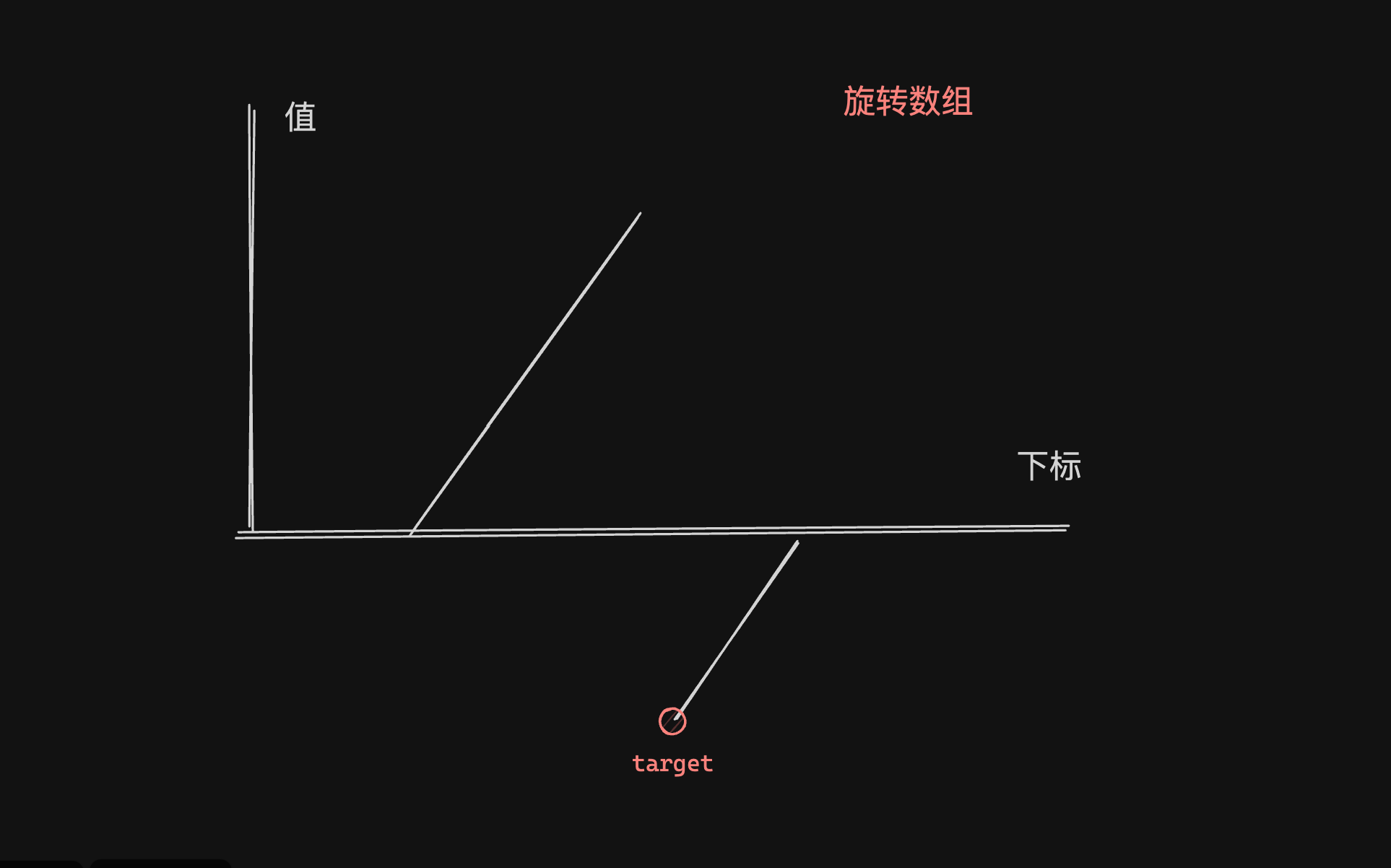
相当于要找到target的值,题目要求使用O(log n)的复杂度,那么单纯的遍历数组就没有办法达到这个了,可以考虑使用二分查找来做。
我们的mid可能有两种情况 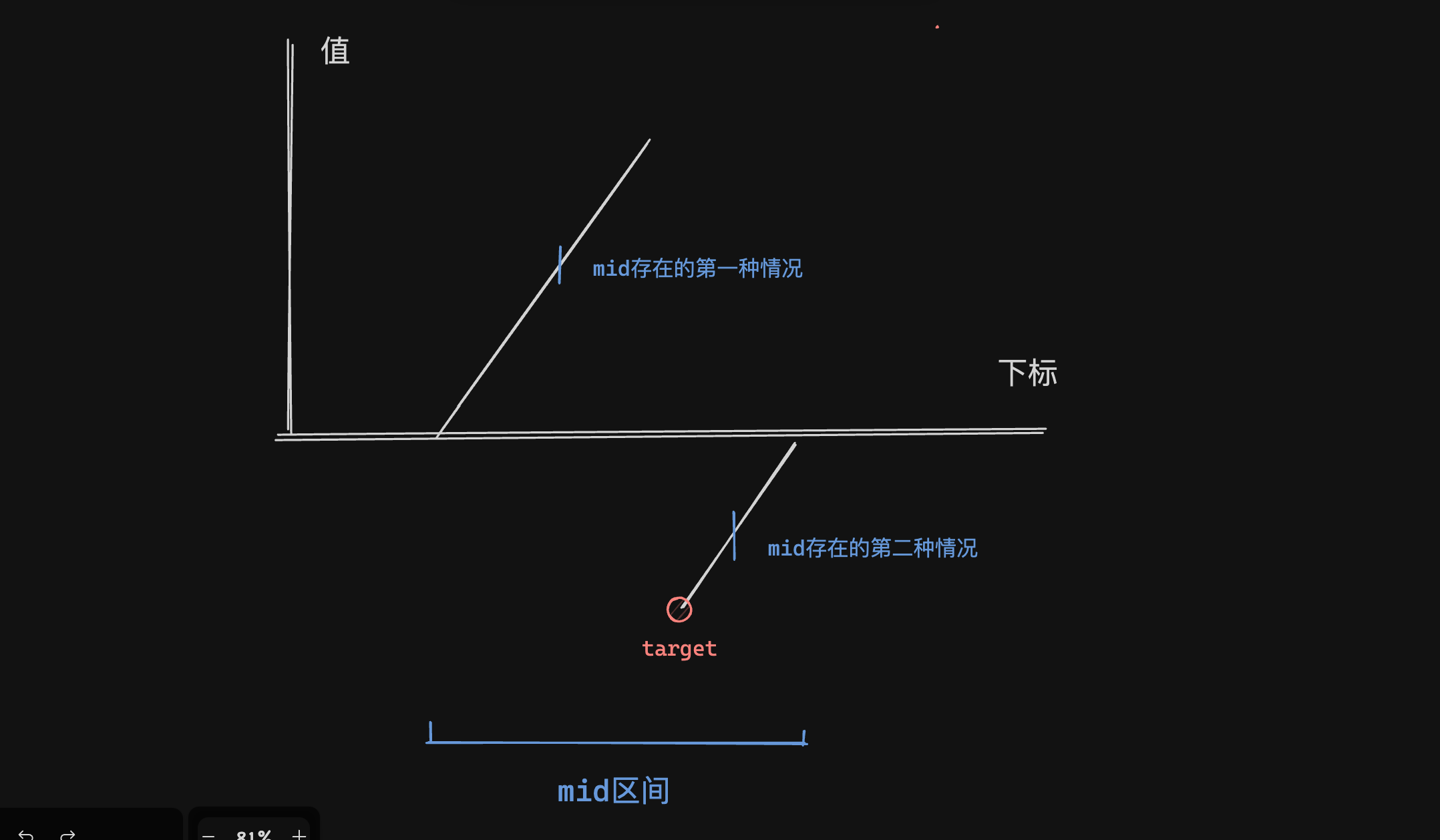
当mid是第二种情况,那么将r = mid不断进行收缩,每次我们收缩的就是一半。
还有一个问题,如何判断mid是在右区间还是左区间呢?因此数组数升序的,用nums[0]作为check函数的判断点。
那么就会有两种情况,第一种nums[0] > mid和第二种nums[0] <= mid,因为有序这个特点,只有在nums[0] < mid的时候才有可能是相等的。在使用二分的时候需要注意,如果使用的是第二种方式进行check函数为true返回答案的时候需要+1。这是因为答案一定是在右区间的,nums[0] <= mid找到的一定是左区间最后一个位置。
二分查找不一定是有单调性才能用,二分本质是两段性
代码
class Solution {
public int findMin(int[] nums) {
if (nums[0] < nums[nums.length - 1] || nums.length == 1) {
return nums[0];
} else {
int l = 0;
int r = nums.length - 1;
while (l < r) {
int mid = (l + r) >> 1;
if (nums[0] > nums[mid]) r = mid;
else l = mid + 1;
}
return nums[l];
}
}
}
class Solution {
public int findMin(int[] nums) {
if (nums[0] < nums[nums.length - 1] || nums.length == 1) {
return nums[0];
} else {
int l = 0;
int r = nums.length - 1;
while (l < r) {
int mid = (l + r + 1) >> 1;
if (nums[0] <= nums[mid]) l = mid;
else r = mid - 1;
}
return nums[l + 1];
}
}
}