BinarySearchTree定义
二叉搜索树是二叉树的一种。
任意一个节点的值都大于其左子树所有节点的值。
任意一个节点的值都小于其右子树所有节点的值。
它的左右子树也是一颗二叉搜索树。
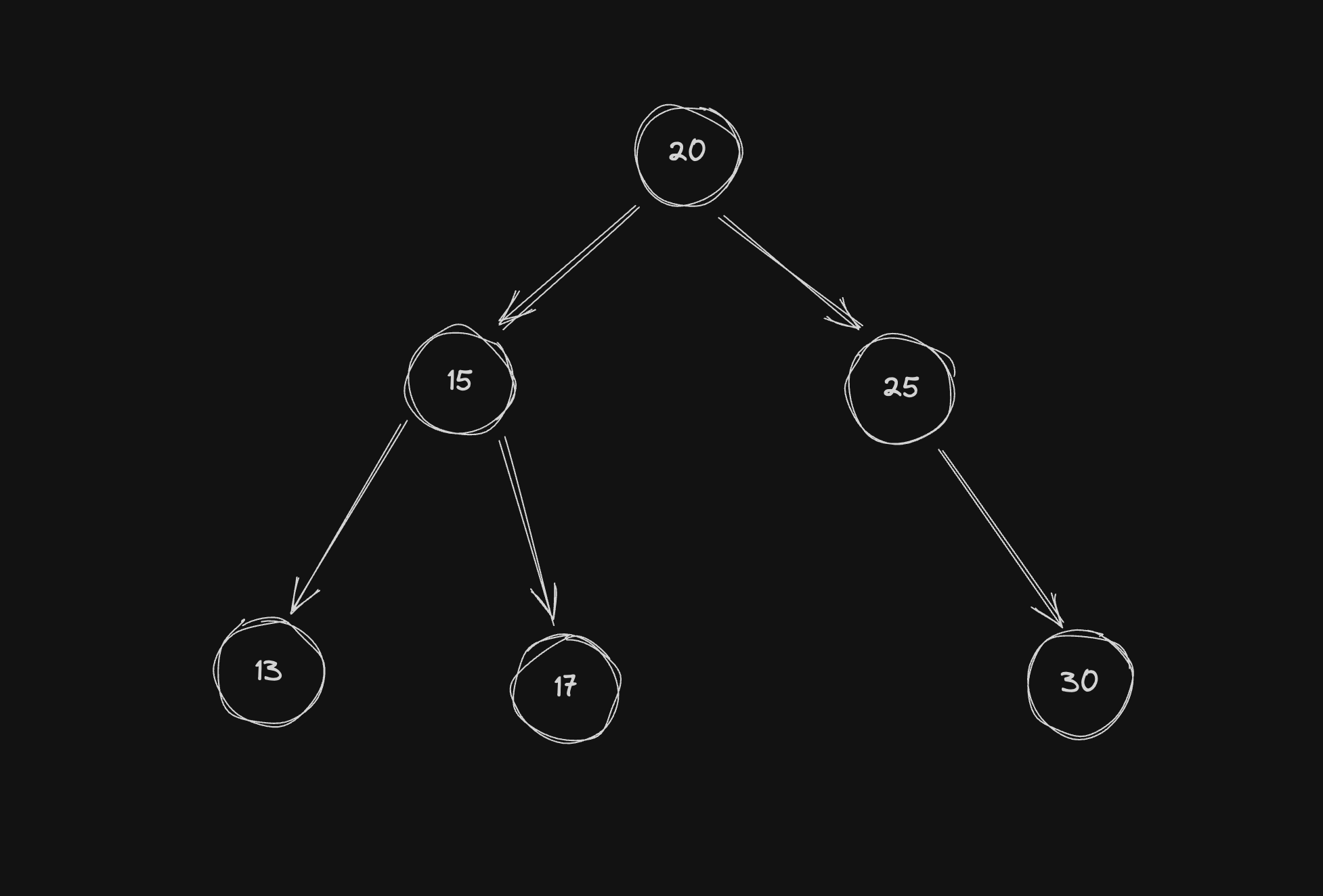
设计一颗二叉树
树中节点的设计
节点的值
左孩子
右孩子
当前节点的父节点
判断当前节点是否为叶子节点
判断当前节点度是否为2
public class Node {
public int element; // 值
public Node left; // 左孩子
public Node right; // 右孩子
public Node parent; // 父节点
/**
* 必须传入当前节点的值以及父节点
* @param element
* @param parent
*/
public Node(int element, Node parent) {
this.element = element;
this.parent = parent;
}
public boolean isLeaf() {
return this.left == null && this.right == null;
}
public boolean NodeDegreeTwo() {
return this.left != null && this.right != null;
}
@Override
public String toString() {
return "Node{" +
"element=" + element +
'}';
}
}
BinarySearchTree Class设计
定义root根节点
定义树的size
add方法 ➕
首先,需要明白的是一颗二叉搜索树的规则是人为规定的, 因此在本次设计中遵守,左子树的值是小于父节点的,右子树的值是大于父节点的。
在实现增加方法的时候,需要严格按照规定的进行增加
首先如果root为null那么直接将新节点作为root即可
根节点不为空,那么需要找到一个节点作为新节点的父节点
找到之后只需要判断插入该节点的左子树还是右子树
重点分析根节点不为空的情况
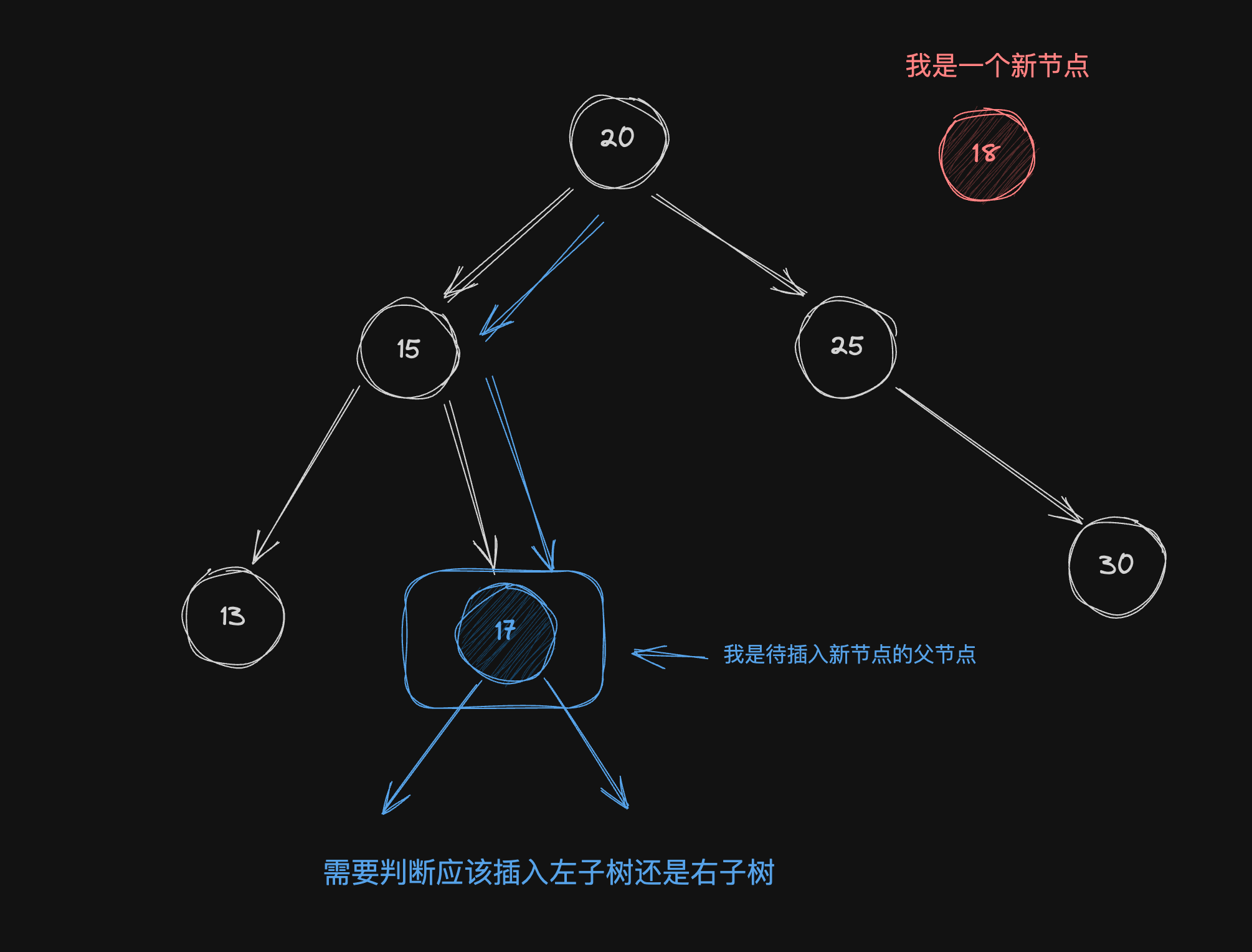
根据上述的示意图,不难发现我们需要两个变量来记录。待插入新节点的父节点,插入的是左子树还是右子树
这是核心代码,当node == null意味着insertParentNode就是待插入新节点的父节点,而cmp变量存放的就是用于判断,插入的是左子树还是右子树
Node node = root;
Node insertParentNode = root;
int cmp = 0; // 记录插入左子树还是右子树
while (node != null) {
insertParentNode = node;
cmp = cmp(node.element, element);
if (cmp == 1) { // node.element > element 左边
node = node.left;
} else { // node.element <= element 右边
node = node.right;
}
}
remove方法 ➖
在实现删除功能的时候,需要保证时刻满足二叉搜索树的性质。
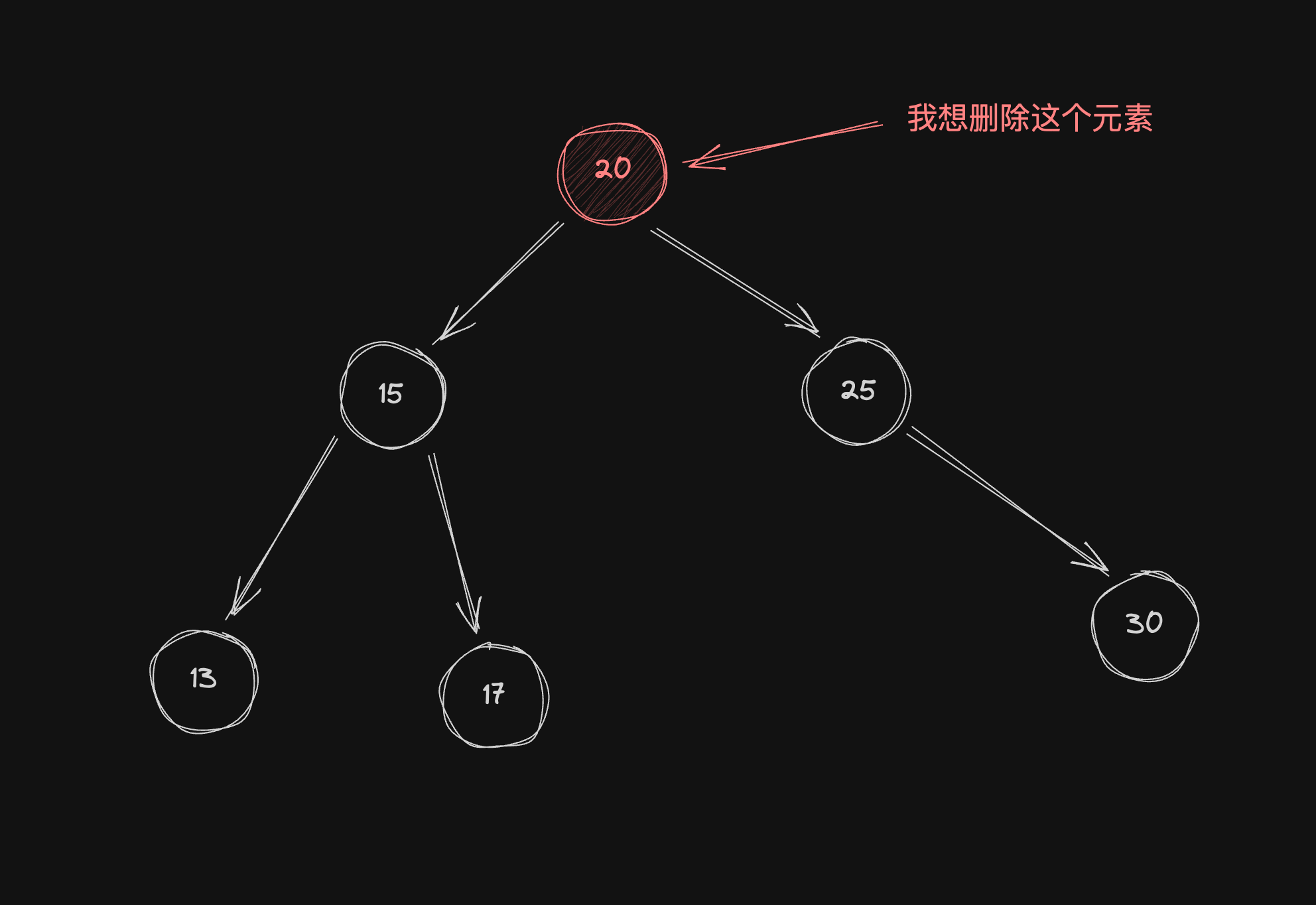
例如:如果我想删除下图的元素,应该怎么做,肯定需要找到一个元素来代替它,代替之后必须满足二叉搜索树的性质,需要用到前驱后继节点
前驱后继节点
前驱后继的定义就是:按照二叉树的中序遍历排列,某个数的前一个节点就为前驱节点,某个数的后一个节点就为后继节点
例如上图,按照中序遍历得到的是13 15 17 20 25 30。那么20的前驱节点就是17,后继节点就是25
利用这个特点,只需要找到前驱或者后继来代替待删除节点即可
实现
如果实现根据任意一个节点找到后继节点呢?(前驱也是一致的)
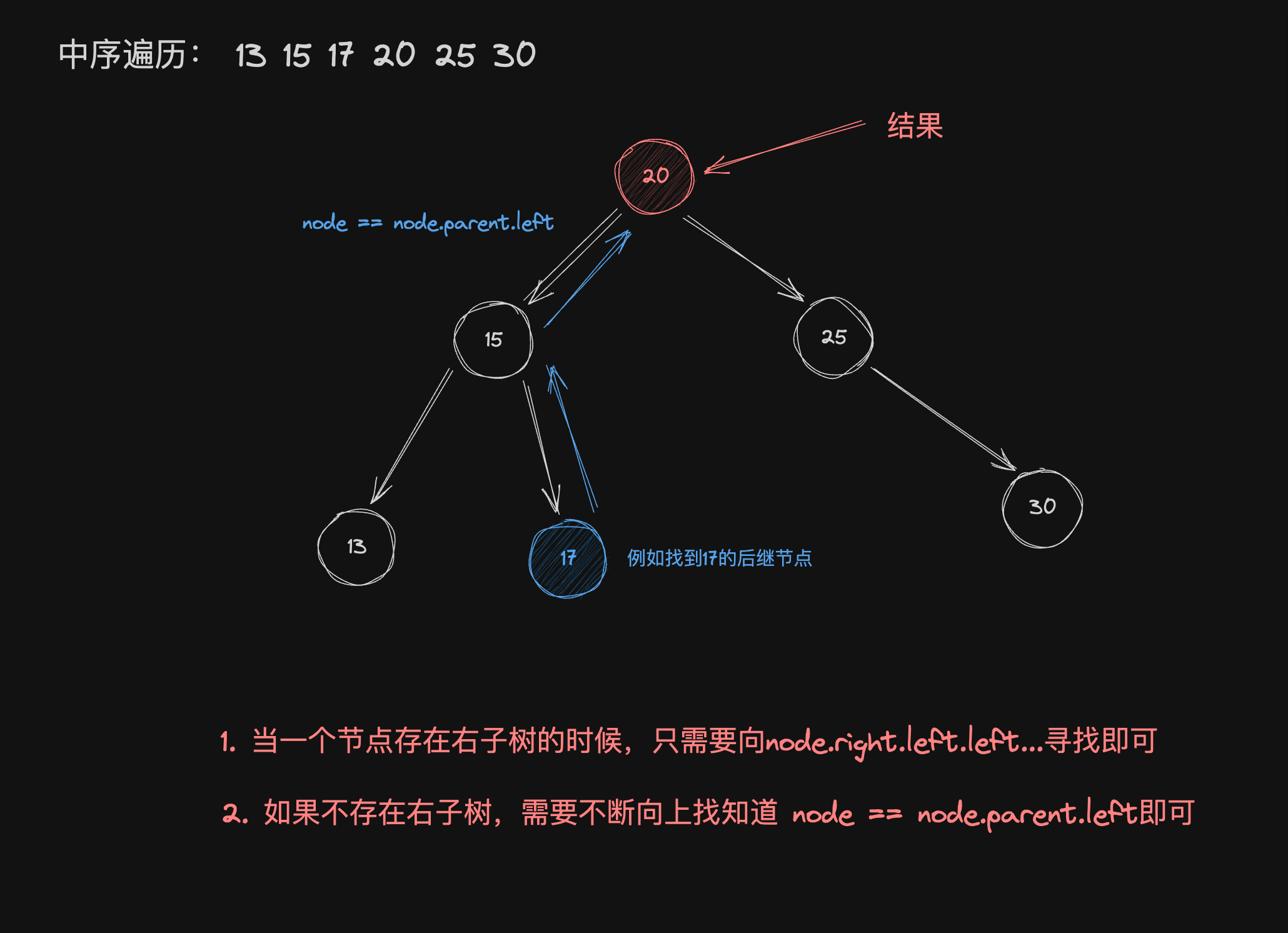
private Node successor(Node node) {
Node p = node.right;
// 存在右子树的情况
if (p != null) { // node.right.left.left...
while (p.left != null) {
p = p.left;
}
return p;
}
// 不存在右子树的情况向上寻找
while (node.parent != null && node != node.parent.left) {
node = node.parent;
}
// 当node == node.parent.left这时候node.parent就是答案节点
// 当node.parent == null无后继直接返回node.parent也是可以
return node.parent;
}
删除元素 — 分类讨论
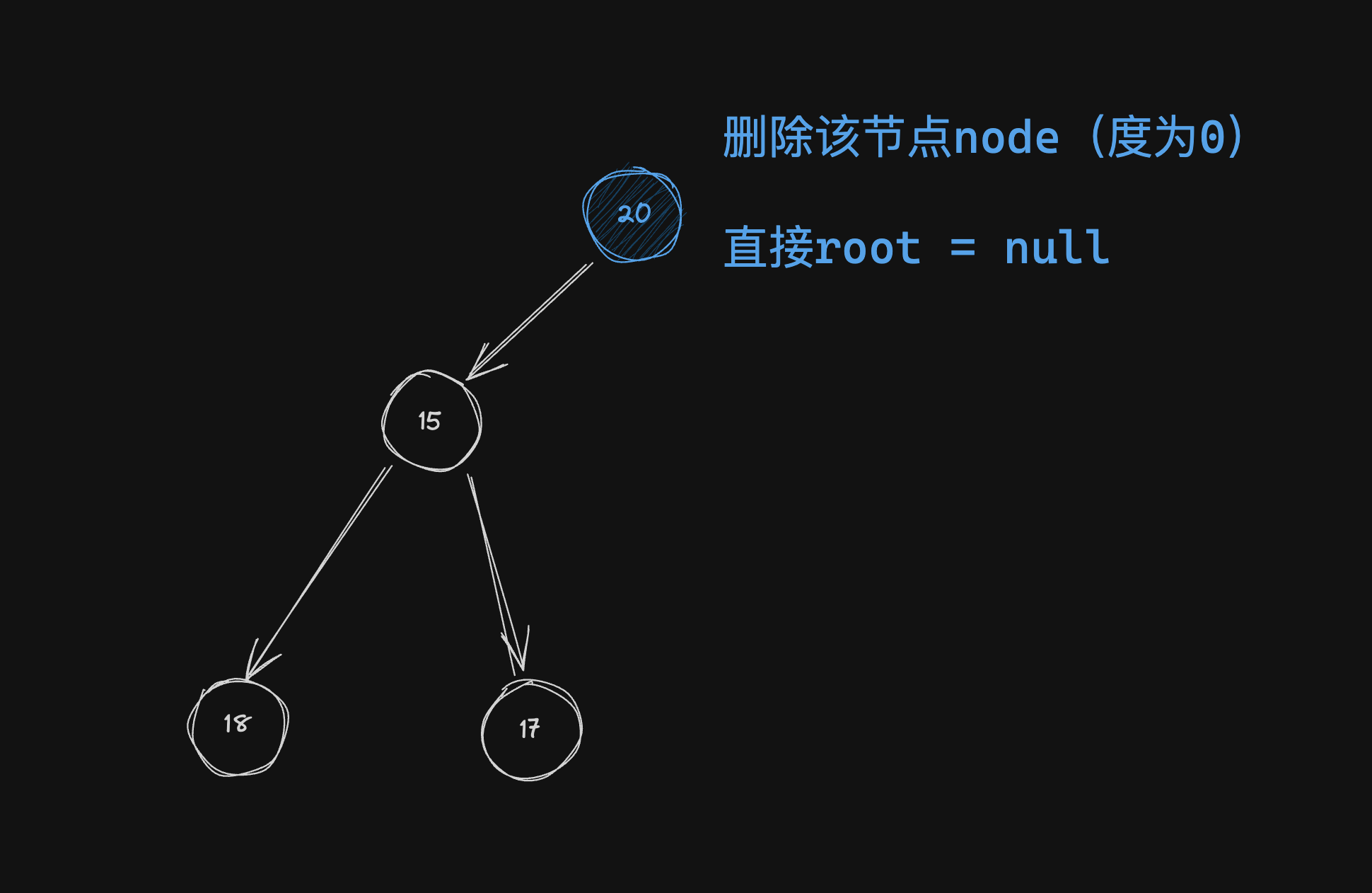
当删除的节点度为0
那么直接将
node.parent.left = null或者node.parent.right = null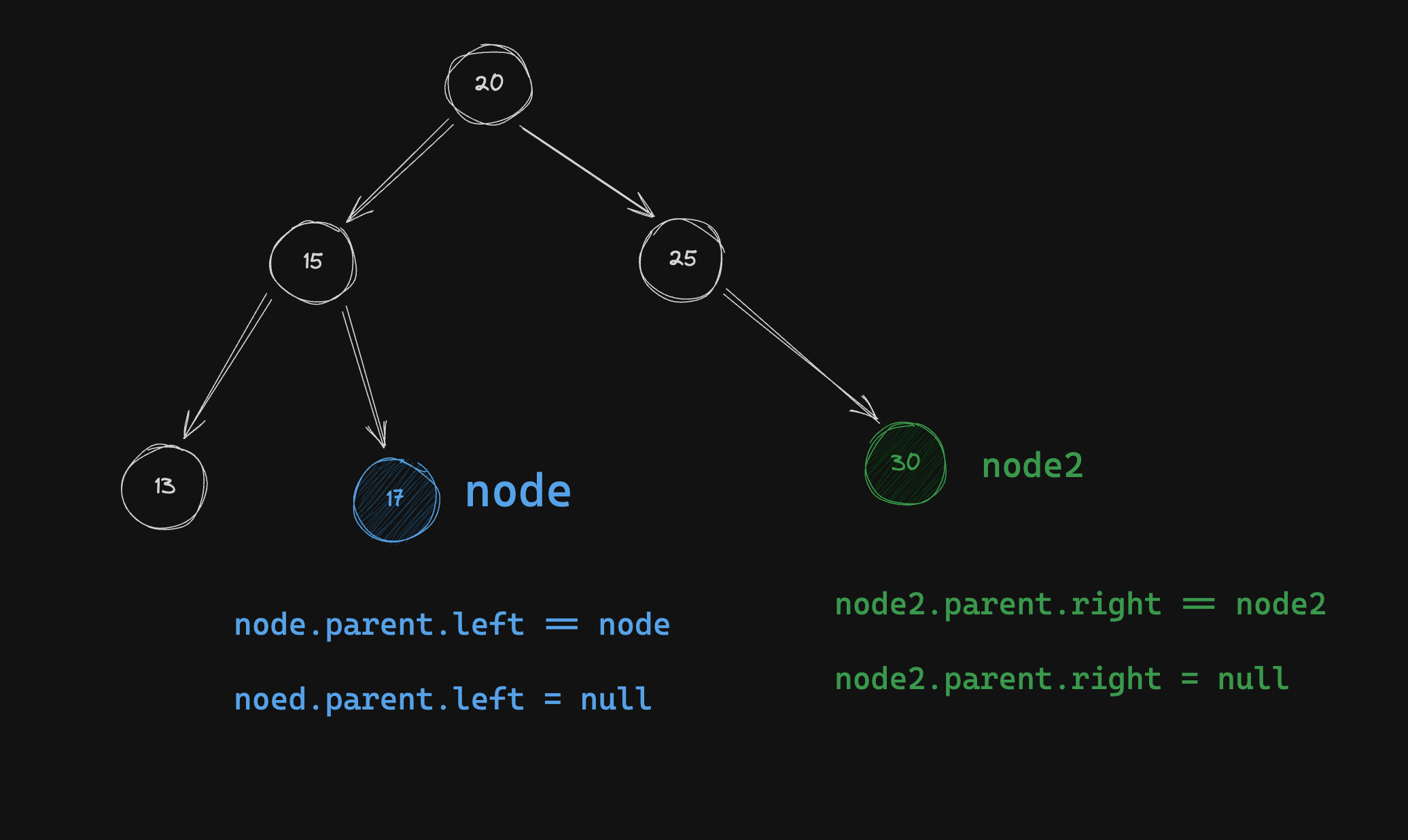
当删除的节点度为1
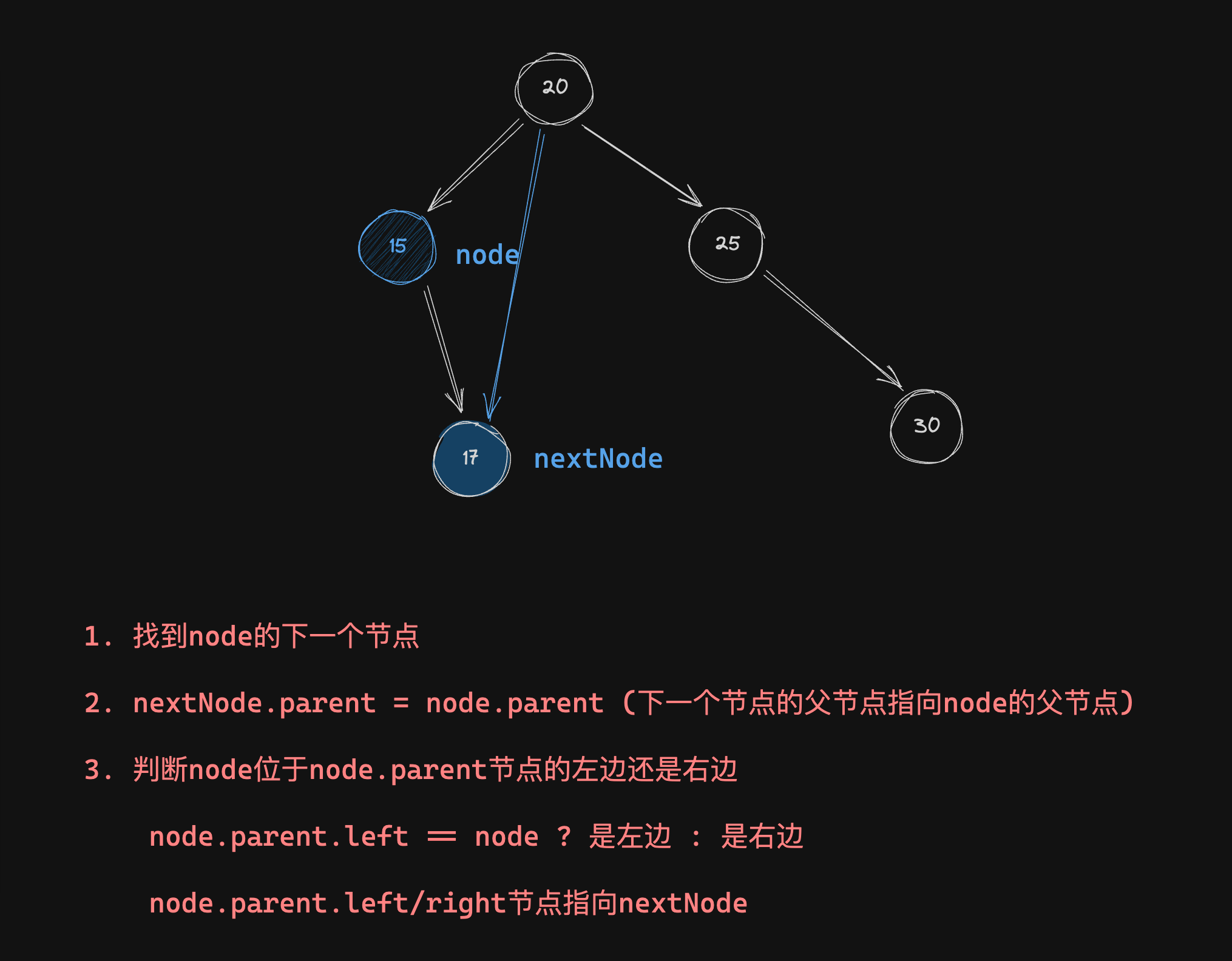
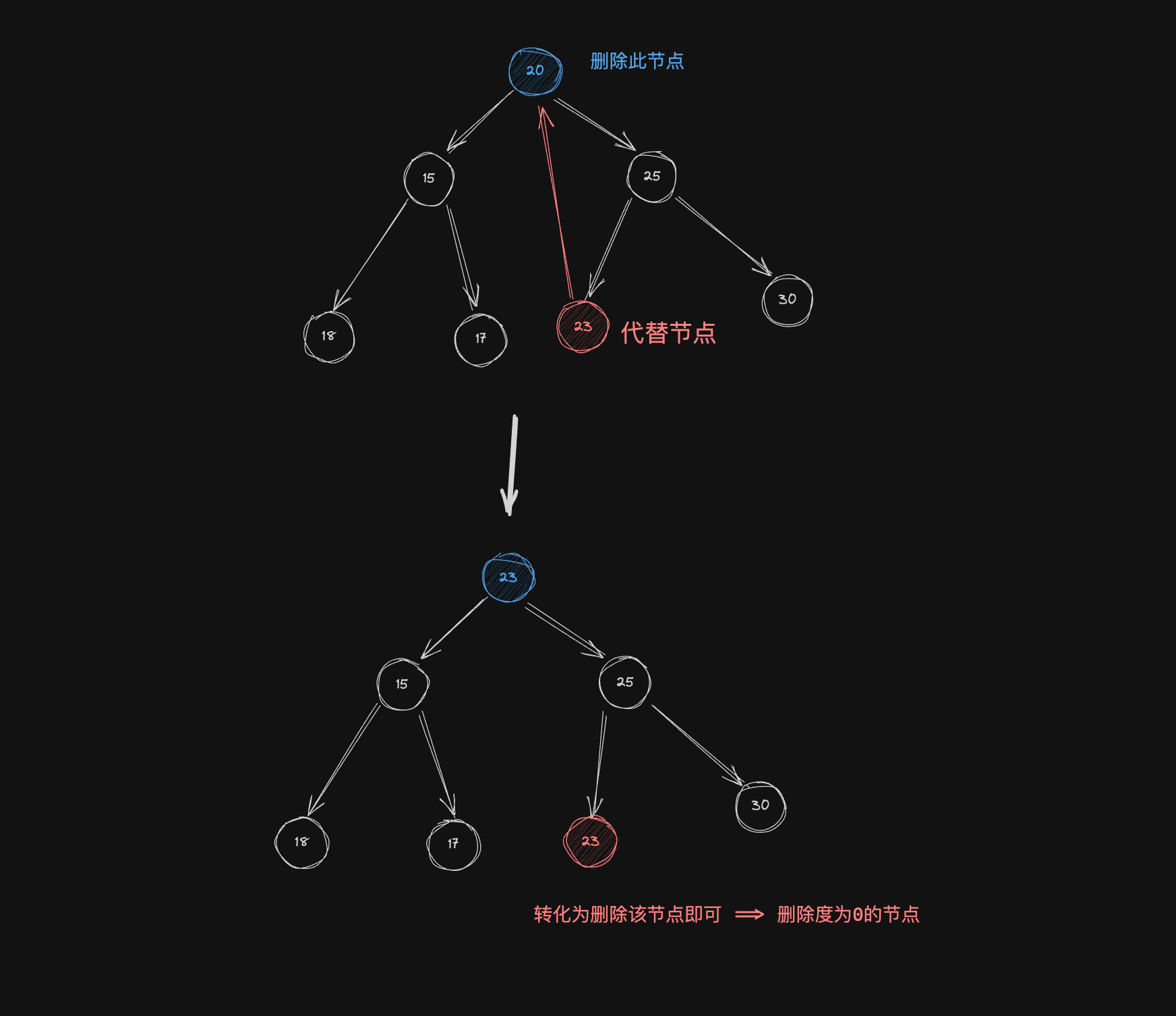
当删除节点的度为2
其实这一种情况就是删除度为1或者度为0,因为我们是直接获取前驱或者后继节点代替它,之后直接处理代替节点即可。
情况一:
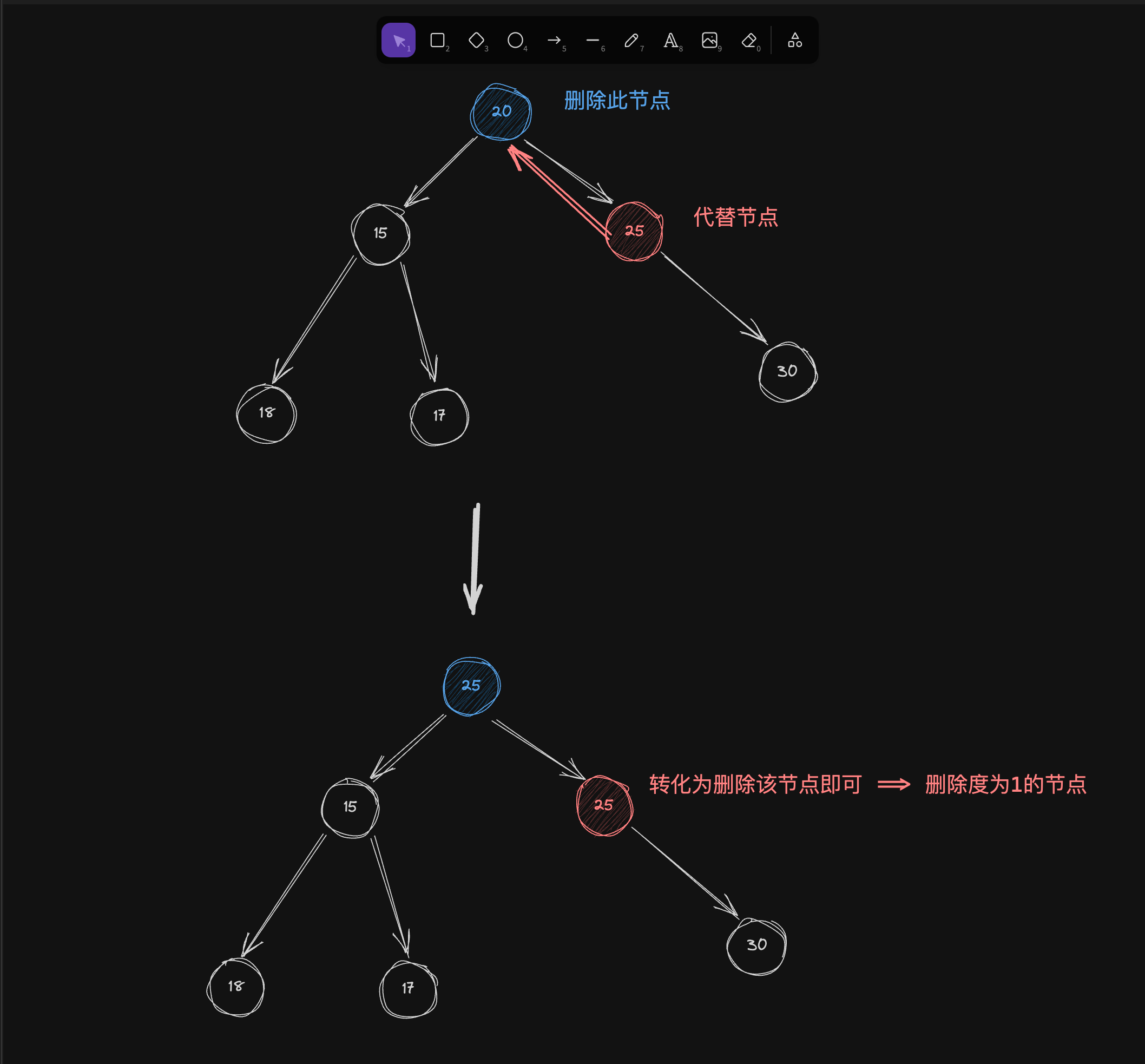
情况二:
边界情况
因为删除度为2的节点,最终可以被归结为删除度为0或者1,下面是核心代码
if (r != null) { // 度为1的情况
// 下一个节点的父节点指向node.parent
r.parent = node.parent;
// node.parent父节点指向下一个节点(判断是左子树还是右子树)
if (node.parent == null) { // 当node父节点为空的话,根节点
root = r;
} else if (node.parent.left == node) { // 是左子树
node.parent.left = r;
} else {
node.parent.right = r;
}
} else if (node.parent == null) { // 删除的节点是叶子节点,且是root节点
root = null;
} else {
// 判断连接左子树还是右子树即可
if (node == node.parent.left) node.parent.left = null;
else node.parent.right = null;
}
if (node.parent == null) {} // 当node父节点为空的话,根节点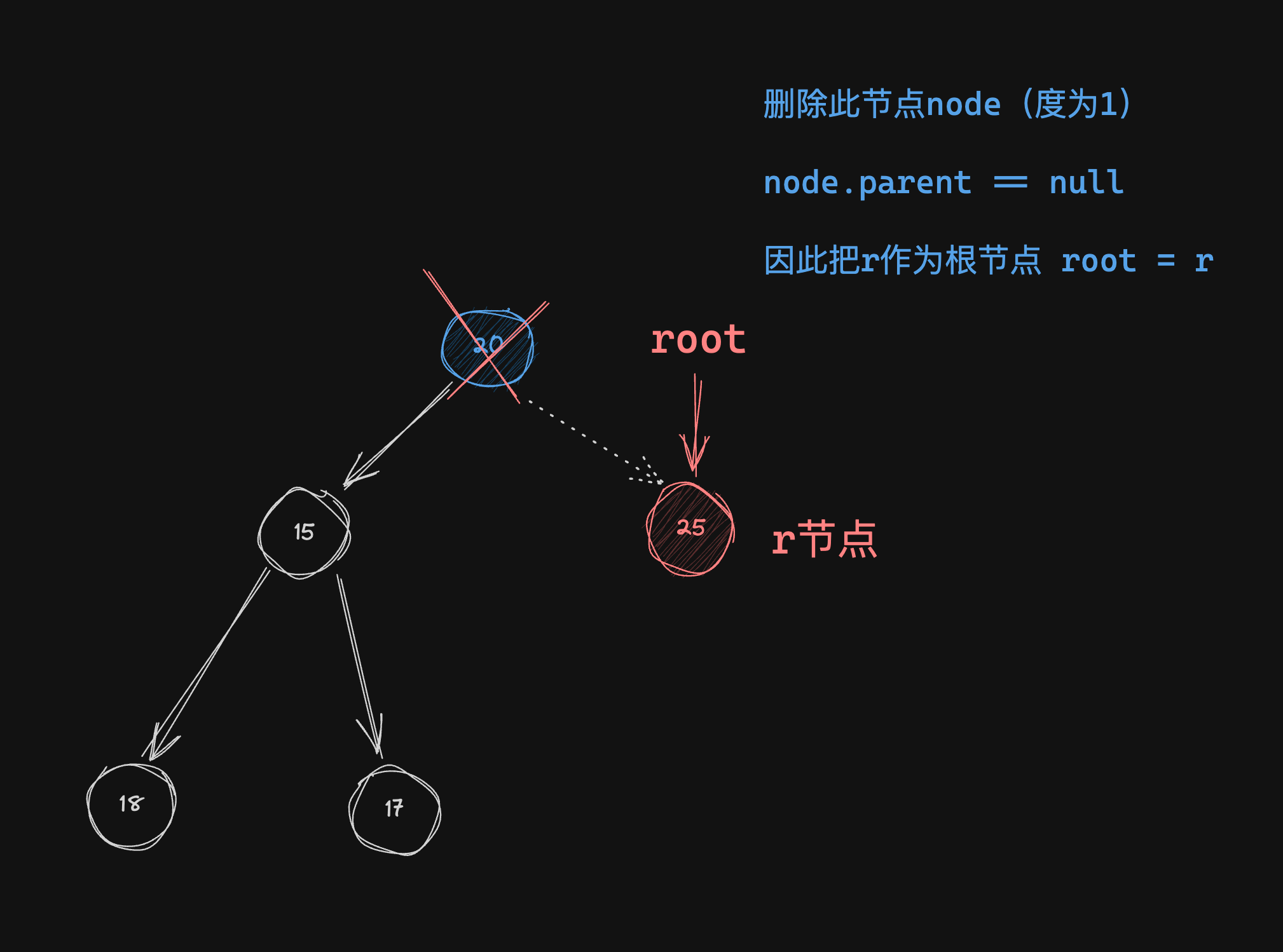
node.parent == null // 删除的节点是叶子节点,且是root节点